ある温度範囲における抵抗値と温度の関係で、式1によって近似的に表されます。
T、Ta: 絶対温度 (K)
R、Ra: T、Taにおけるゼロ負荷抵抗値 (Ω)
B :B定数 (K)
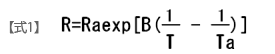
サーミスタは一定の温度で抵抗値を測定し、自己発熱による抵抗値変化が無視出来るような十分低い消費電力で測定した場合の抵抗値をゼロ負荷抵抗値といいます。
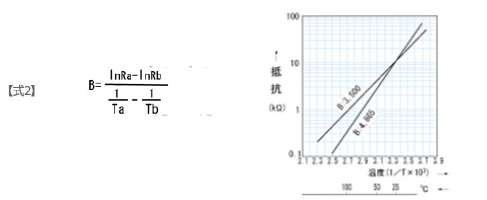
抵抗一温度特性で任意の2点の温度から求めた抵抗値変化の大きさを表す定数で、式2によって表されます。
この特性をIogRと1/Tでグラフ化すると、ほぼ直線で表すことが可能です。
任意の温度での1℃当たりのゼロ負荷抵抗値の変化率を表す係数で、式3で表されます。
α:抵抗温度係数 (%/K)
T:任意の絶対温度 (K)
R:T(K)におけるゼロ負荷抵抗値 (Ω)
B:B定数 (K)
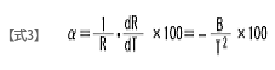
熱平衡状態でサーミスタ素子の温度を、自己発熱によって1℃上げるために必要な電力を表す定数で、サーミスタの消費電力と素子の温度上昇の比で求めます。
サーミスタの消費電力をP(mW)とすると
P=δ(Tb-Ta)から
δ=P/(Tb-Ta)=I2R/(Tb-Ta)
P:サーミスタの消費電力 (mW)
δ:熱放散定数 (mW/℃)
Ta:サーミスタの周囲温度 (℃)
I:サーミスタに流れる電流 (mA)
Tb:サーミスタが温度上昇して熱平衡状態になった時のサーミスタの温度 (℃)
R:Tb(℃)時のサーミスタ抵抗値 (Ω)
ゼロ負荷の状態でサーミスタの周囲温度を急変させたとき、サーミスタの素子の温度が最初の温度と最終到達温度との温度差の63.2%変化するのに要する時間を表す定数です。
熱時定数(τ)をn倍したときの値は
τ=63.2% 2τ=86.5% 3τ=95.0%
のようになります。
サーミスタは抵抗器である為、電力が加わると発熱をします。
この様子がサーミスタ自身を温めているように見えるため、自己発熱と呼んでいます。
温度上昇を⊿T(℃)とした場合、⊿T=P/σ(℃)
サーミスタは小さい為、電力Pの単位はmWを使い、σの単位はmW/℃となります。
定格周囲温度(一般に25℃)で連続してサーミスタに負荷出来る電力の最大値(mW)です。
サーミスタに電圧を印加すると自己発熱していき、周囲の温度に応じた熱平衡温度に達しますが、過大な電力によって熱暴走したり、事故発熱の度合いによっては特性破壊されることもあるため、連続して負荷出来る電力の上限として定められています。
Surface Mount Device(表面実装部品)の略称であり、プリント基板の表面にはんだ付けのみによって実装することのできるように製造された電子部品のこと。
Negative Temperature Coefficient Thermistorの略称であり、温度の上昇で抵抗値が減少するサーミスタのこと。
Positive Temperature Coefficient Thermistorの略称であり、温度の上昇で抵抗値が増加するサーミスタのこと。